Скачать с ютуб Lesson 2: Practical Deep Learning for Coders в хорошем качестве

Lesson 2: Practical Deep Learning for Coders

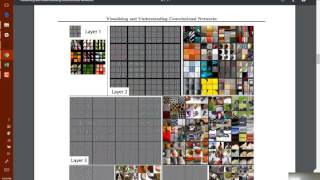
CONVOLUTIONAL NEURAL NETWORKS For last week’s assignment your goal was to get into the top 50% of the Kaggle Dogs v Cats competition. This week, Jeremy shows his answer to this assignment. It’s a good idea to spend a few hours giving the assignment your best shot, prior to watching this lesson, since it’s the process of trying, failing, and trying again that is the basis of learning the practical skills needed to be a deep learning practitioner. After showing how to submit a successful entry to this competition, we then learn some critical information about the loss function most commonly used for classification projects, as well as seeing how to use visualization to understand where your model is succeeding and failing. In the second half of the lesson, we dig into the details of CNNs and fine-tuning. We start by discussing why we normally want to start with a pre-trained network, rather than starting with random weights, and see how fine-tuning keeps those layers that contain useful features for our model, and updates the weights of those layers that are less suitable. We develop an understanding of how and why fine-tuning works, including learning about three of the key foundations of neural networks: Dense (or “fully connected”) layers Stochastic gradient descent (SGD) Activation functions (or “non-linearities”)